There is a set of built-in 3D objects (box, sphere, etc.). You can also create your own 3D objects, and even change their shapes dynamically, as in the case of the example program shown above, in which a pulse moves up along a rug.

The surface of an object consists of a mesh of triangles, and a triangle consists of 3 vertices. We can create a triangle by first creating three vertex objects, then using them to form a triangle:

a = vertex( pos=vec(0,0,0) )
b = vertex( pos=vec(1,0,0) )
c = vertex( pos=vec(1,1,0) )
T = triangle( v0=a, v1=b, v2=c )

Equivalently, one could write this:

T = triangle(
          v0=vertex( pos=vec(0,0,0) ),
          v1=vertex( pos=vec(1,0,0) ),
          v2=vertex( pos=vec(1,1,0) ) )

Another option is to give a list of vertex objects:

T = triangle( vs=[a,b,c] )

Often it is convenient to divide a surface into rectangles instead of triangles, which is done with a quad object. The following statements are equivalent to creating two triangles with vertices (a, b, c) and (a, c, d):

a = vertex( pos=vec(0,0,0) )
b = vertex( pos=vec(1,0,0) )
c = vertex( pos=vec(1,1,0) )
d = vertex( pos=vec(0,1,0) )
Q = quad( v0=a, v1=b, v2=c, v3=d )

You could also write this:

Q = quad( vs=[a,b,c,d] )

The vertices of a triangle or quad can have their own colors, which are blended between vertices:

                 

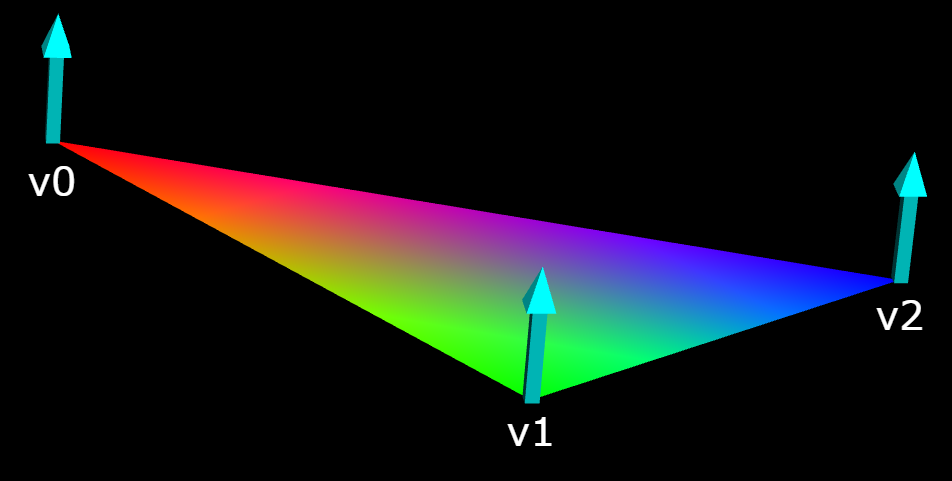
The role of the "normals", shown here as arrows perpendicular to the plane of the triangle, is discussed in detail below. If you point the thumb of your right hand in the direction of the normal, and curl the fingers of your right hand, your fingers should go from v0 to v1 to v2. To put it another way, looking down the normals from above, going from v0 to v1 to v2 should go counterclockwise.

The power of triangles and quads

There are two powerful capabilities of triangles and/or quads: First, any surface can be approximated by a mesh of triangles, so you can make any shape you like. Second, by changing the attributes of vertex objects, you can change the shape of a surface dynamically. A vertex object can be shared by several adjacent triangles, and changing that vertex object simultaneously affects all of the triangles that include that vertex object.

In the rug example pictured above, the rug is divided into a rectangular mesh of vertex objects, and quad objects are created from these vertex objects. The same vertex may be shared by as many as four adjacent quad objects. Changing the z position of a shared vertex object affects all those quads that refer to that vertex, which makes it easy to create a moving pulse simply by modifying the vertex positions. In the rug program the quad objects are needed to display the rug, but once the quads have been created all further calculations refer just to the underlying vertex objects.

For a triangle or quad, in addition to specifying vertex objects you can specify texture and/or visible, but the usual attributes for other objects such as pos or color don't apply; this information is specified in the vertex objects. (It is not possible to specify place, flipx, flipy, or turn for a triangle or quad texture. These effects can be achieved by the way texpos is specified in the vertex objects.)

If you wish to specify a bumpmap to go with a texture, use the same scheme used with other objects. This example assumes that you have specified texpos values in the vertex objects (see below):

quad(vs=[a, b, c, d],     texture=dict(file=textures.stones,                  bumpmap=bumpmaps.stones))

If you prefer, you can create the dictionary like this::

quad(vs=[a, b, c, d],     texture={'file':textures.stones,              'bumpmap':bumpmaps.stones))

Display speedup: Typically you will use many triangles to create a complex object. For clarity you might wish to keep them all in a list: tris = [ triangle1, triangle2, ....]. If the object's internal shape need not change (unlike the case of the rug), you can say "s = compound(tris)" in which case you can move and resize and rotate the object "s" very rapidly, just as though it were a built-in object such as a sphere.

Vertex attributes

The attributes of a vertex object are pos, normal, color, opacity, texpos, bumpaxis, shininess, and emissive. The pos attribute represents the location of the vertex in 3D space.

The attributes color, opacity, shininess, and emissive are the same as those for other objects such as box or sphere, but within a triangle they are averaged among the three vertex objects. For example, at locations between a red vertex and a green vertex there is a fade from red to green. A striking effect occurs if two of the three vertex objects have opacity = 0, because as you approach the edge of the triangle bounded by those two vertices the triangle fades to nothing.

The vertex attributes normal, texpos, and bumpaxis require additional explanation..

normal: The lighting of a triangle, based on its own color and the lights provided, is calculated based on the "normals" to the triangle, vectors pointing away from the surface of the triangle. In the simplest case, the normal at each vertex is perpendicular to the surface of the triangle, as shown in the figure above.

Each triangle has three normals, at each of the three vertices. The normal at each interior point of the triangle is an average of the three specified normals.

Where two triangles meet, you will see a sharp break if the two triangles have different normals. If you want to smooth the transition, you should average the neighboring normals (n1+n2)/2 and apply them to both triangles; this will smooth out the joint.

If you don't explicitly specify a normal for a vertex, the normal is given the default value vec(0,0,1), pointing out of the screen. If the vertex is to be used in a triangle that does not lie in the xy plane, you need to specify a normal yourself. If the three vertices are a, b, and c (in counter-clockwise order), and you want normals that are perpendicular to the triangle, you can calculate the normal like this:

(b-a).cross(c-b).norm()

The "vector cross product" produces a vector that is perpendicular to the plane defined by the two vectors b-a and c-b, the first two edges as you go around the triangle. If the fingers of your relaxed right hand curl in the direction a to b to c, your outstretched thumb points in the direction of the vector cross product.

texpos: If you intend to apply a texture or bumpmap to a mesh object, you must specify in the mesh how you want the texture to be mapped onto your object. You might want the texture to occupy only a portion of the object, or be stretched or distorted in some way. This is done by specifying "texel" coordinates, given as texpos vectors in the vertex objects.

Texel coordinates for a surface texture are specified by an "x" and a "y", both ranging from 0 to 1 if the entire texture is to be displayed, left to right and bottom to top. (In many discussions texel coordinates are referred to as "u" and "v", or as "s" and "t".) In anticipation that WebGL will eventually enable 3D textures, which permit filling a textured volume, GlowScript requires that in texpos elements the third component must be zero.

For example, to fill a quad with a texture, the texpos vectors in the vertex objects v0, v1, v2, and v3 would be vec(0,0,0), vec(1,0,0), vec(1,1,0), vec(0,1,0), no matter what the 3D pos attributes are. If you want only the lower quarter of the texture to fill the quad, the texpos vectors would be vec(0,0,0), vec(0.5,0,0), vec(0.5,0.5,0), vec(0,0.5,0). Note that <0,0,0> is at the lower left, and <1,1,0> is at the upper right.

bumpaxis: If you will use a bumpmap, you need to specify a vector bumpaxis direction for each vertex, specifying the direction of the "x" axis of the texture at that location. The default bumpaxis is vector(1,0,0).

Important limitation: WebGL currently supports no more than 65536 vertex objects. However, when you compound an object involving vertex objects, any vertex objects that are not used in other objects are are freed up to be re-used.

Mouse picking of triangles/quads

The operation scene.mouse.pick() gives the object lying under the mouse. It may be convenient to specify my_id='car' as your own attribute for each triangle or quad in the object, so that you can tell whether the triangle or quad is part of the 'car' group:

t1 = triangle(... my_id='car')
t2 = triangle(... my_id='car')
...
obj = scene.mouse.pick()
if (obj != null and
    obj.my_id != undefined and
    obj.my_id == 'car') hitcar = True